Servomechanismus S2

Hlavní stránka	Laboratorní modely	Vyučované předměty	Vybavení	Historie	Správce laboratoře	Pro studenty	Odkazy

Základnem tohoto laboratorního přípravku je model servomechanismu IfA – 122, současná podoba je výsledkem úprav z roku 2007 Alexandrem Cillerem v rámci jeho bakalářské práce <ref name="ciller">CILLER, Alexandr. Servomechanismus s proměnným tlumením, 2007</ref> a z roku 2009, kdy úpravy dokončil Adam Hořčica <ref name="horcica">HOŘČICA, Adam. Servomechanismus s proměnným tlumením, 2009</ref>. Model Servomechanismus S2 je využíván pro řízení rychlosti a úhlu natočení servomechanismu (např. pomocí PID regulátorů, lead – lag regulátorů). V praxi se se systémy simulovanými tímto modelem setkáváme v mnoha situacích, např. při zkoumání rychlostních a pozičních řídicích systémů. Regulace pozice (úhlu natočení) a rychlosti jsou v praxi používané u mnoha systémů, např. u různých robotů, manipulátorů apod. Využití najdeme také v dopravě, letectví, medicíně apod. Fotografie laboratorního modelu je na obr. 1.

• 

  Obrázek 1: Servomechanismus S2

Schéma a konstrukce modelu

Model servomechanismu S2 je tvořen 2 částmi: vlastním modelem servomechanismu a přístrojovou skříní.

Vlastní model servomechanismu

Vlastní model s popisem jednotlivých částí znázorňuje obr. 2 a tab. 1.

• 

  Obrázek 2: Popis částí vlastního modelu S2

Tabulka 1: Popis částí vlastního modelu S2

označení v obrázku	část
1	výměnný kotouč
2	ložisko
3	tlumící kotouč
4	převodovka
5	motor s tachodynamem
6	ukazatel otáček
7	potenciometr - rychlost otáčky
8	motor pro nastavení tlumení
9	IRC
10	pevná spojka

Základem modelu je stejnosměrný motor, na jehož hřídeli je tachodynamo, kterým lze měřit rychlost otáčení motoru, jeden ze 3 výměnných disků (parametry jednotlivých disků uvedeny v tab. 16), kterými se mění moment setrvačnosti, převodovka, kotouč setrvačníku a disk magnetického tlumení. Úroveň tlumení lze regulovat pomocí pohyblivého magnetu ovládaného druhým motorem. Tlumení je způsobeno vířivými proudy, které vznikají v hliníkovém disku. Model je též vybaven dvěma ukazateli:

Ukazatel úhlu natočení hřídele S modelem je spojen přes převodovku (1:60), tak že na jednu otáčku ukazatele se hřídel otočí právě 60 krát. Zároveň je ukazatel spojen s potenciometrem s přerušením dráhy na úhlu 0°, který je využit pro snímání výstupního úhlu natočení.

Ukazatel zadání požadovaného úhlu natočení resp. otáček hřídele Tento ukazatel je využíván pro ruční řízení rychlosti a úhlu natočení servomechanismu.

Akční veličiny představují u (vlastní motor servomechanismu) a u_d (motor pro nastavení úrovně tlumení).

Přístrojová skříň se zdrojem a zesilovačem

Výkonový zesilovač představuje řízený zdroj napětí, který výkonově zesiluje signál z měřící karty. Zdroj zajišťuje napájení potenciometrů, pomocí nichž rozvažujeme napětí následně snímaná měřící kartou. Model je spojem s PC pomocí karty MF614. Model se zapíná spínačem na levé straně přístrojové skříně. Přístrojová skříň je zobrazena na obr. 3.

• 

  Obrázek 3: Přístrojová skříň modelu S2

V tab. 2 jsou uvedeny konkrétní technické parametry modelu.

Tabulka 2: Technické parametry modelu S2

veličina	hodnota	jednotka
nominální napětí motoru	10	V
nominální proud motoru	2,5	A
odpor vinutí kotvy	6,2	W
indukčnost vinutí kotvy	0,75	mH
moment setrvačnosti bez závaží	3.10-6	kg.m2
konstanta tlumení	3.10-5	N m s rad-1
momentová konstanta motoru	32.10-3	M m A-1
konstanta tachodynama	27,11	rad s-1 V-1

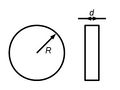
Další důležité parametry se týkají vyměnitelných disků. Jsou zaznamenány v tab. 3, význam veličin zobrazuje obr. 4.

• 

  Obrázek 4: Význam parametrů vyměnitelného disku

Tabulka 3: Technické parametry modelu S2

disk č.	d [mm]	R [mm]	m [kg]	J [kg m2]
1	10	28	0,193	75,6.10-6
2	20	34	0,578	330,5.10-6
3	28,6	44,5	1,401	1,387.10-3

Informace pro studenty

Obecné informace

Při volbě výstupní veličiny úhlová rychlost ω(t) je systém lineární stabilní. Druhá možnost je volit jako výstupní veličinu polohu (úhel) φ(t), jež je integrací rychlosti, tj. v laplaceově transformaci dělíme laplaceovým operátorem, potom systém popisuje přenos s astatismem, tzn. že systém je nestabilní. Model servomechanismu je možné řídit pomocí PC s programem Matlab/ Simulink a Real Time Toolboxu, kde jsou všechny veličiny převedeny na bezrozměrná čísla obvykle v intervalu (-1, +1).

Pokyny pro práci s modelem

• Měřicí kotouč výstupní polohy je pouze přilepen. Netočte za něj!

Důležité vztahy

Model lze z fyzikálního hlediska rozdělit na 2 části jak je patrné z obr. 5: mechanickou a elektrickou. V mechanické části jsou zahrnuty součty jednotlivých momentů, elektrická část vychází z 2. Kirchhoffova zákona, který říká, že algebraický součet napětí ve smyčce je roven nule.

• 

  Obrázek 5: Náhradní schéma modelu S2

Pro matematické vyjadření modelu vycházíme z náhradního schématu (obr. 5), kde u(t)[V] je vstupní napětí na motoru, i(t)[A] je proud kotvou, ω(t)[rad s^-1] je úhlová rychlost hřídele, φ(t)[rad] je úhel natočení hřídele, L[H] je celková indukčnost kotvy, R[Ω] je odpor kotvy, J[kg m²] je moment setrvačnosti, J₀[kg m²] je setrvačnost hřídele, J_d[kg m²] je setrvačnost námi použitého disku č. 2, B  [N m s rad^-1] je tlumení, B₀[N m s rad^-1] je tlumení, k_m[N m A^-1] je momentová konstanta motoru, k_ω[rad s^-1 V^-1] je konstanta tachodynama.

Rovnice elektrické smyčky podle obr. 5 je
<math>u(t)-E(t)=R\,i(t)+J\frac{\mathrm{d}i(t)}{\mathrm{d}t}</math>     (1)

a zároveň elektromotorická síla motoru je dána vztahem
<math>E(t)=k_m \, \omega (t)</math>.     (2)

Závislost mezi elektrickou a mechanickou částí motoru vyjadřuje vztah pro točivý moment M_m, který je produkován motorem:
<math>M_m=k_m \, i(t)</math>.     (3)

V každém časovém okamžiku platí:
<math>M_m=M \, + \, M_z \, + \, M_{B0}</math>,     (4)

kde

M [N m] je moment vyvolaný setrvačností rotující části, M_z [N m] je zatěžovací moment magnetického kotouče, M_BO [N m] je brzdný moment způsobený tlumením.

Pro M_BO platí
<math>M_{B0}=B_0 \, \omega (t)</math>.     (5)

Moment M_z se mění nelineárně v závislosti na otáčkách motoru ω(t). Vztah linearizujeme aproximací přímkou:
<math>M_z=B \, \omega (t)</math>.     (6)

Použitím 2. Newtonova zákona pro rotaci lze pro M definovat rovnici
<math>M=J\frac{\mathrm{d}\omega(t)}{\mathrm{d}t}</math>,     (7)

kde pro celkový moment setrvačnosti J plati
<math>J=J_0 \, + \, J_d</math>.     (8)

Dále platí vztah
<math>\frac{\mathrm{d} \varphi(t)}{\mathrm{d}t}=\omega(t)</math>.     (9)

Volba vstupních a výstupních veličin systému

Jako vstupní veličinu volíme vstupní napětí u(t), výstupní veličinu volíme, jak již bylo řečeno v obecných informacích, buď úhlovou rychlost ω(t) nebo polohu (úhel) φ(t).

Soubory

• Média:S2-id.pdf - zadání pro identifikaci laboratorního modelu
• Média:S2-reg.pdf - zadání pro řízení laboratorního modelu

Literatura

<references/>