Dp 336 en
Individual Pole Placement Via Linear Quadratic Optimization
Author: Cigler Jiří
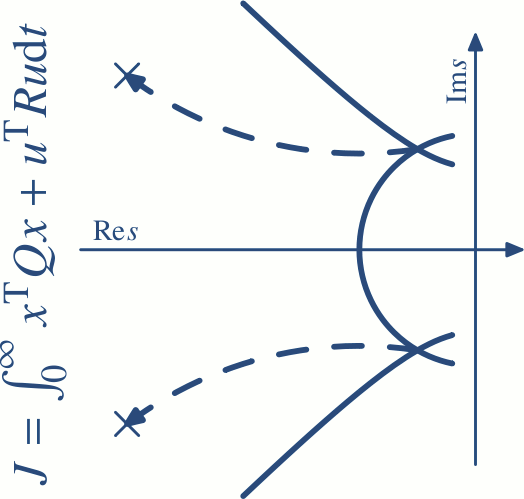
A quadratic optimization is an appropriate tool for designing linear multivariable control systems. However the dynamics of the resulting closed loop is very important for the evaluation of control quality. The dynamics is determined by the positions of closed-loop poles. The relationship between the weighting matrices in quadratic criteria and location of the closed-loop poles of the optimal control system is not clear, transparent and unique. A method for shifting open loop poles to prescribed closed loop locations via choosing appropriate matrices in quadratic performance index is presented. This method is iterative -- only one real pole (or complex conjugate pair of poles) is shifted at each step. Other poles remain in the original positions. Poles could not be shifted to an arbitrary location. The type of shifted pole defines constraints for the desired shift. Mathematical formulas representing such constraints will be presented and several examples will illustrate the shape of the region into which the poles can be shifted. The allowable shifts may result in a faster and dampening feedback. Numerical examples are given to illustrate the simplicity of the presented method.
- Cigler Jiří, tel: +420 776 232 214, mailto:jirkacigler@gmail.com